
Loading Runtime
A t-test is a statistical test used to compare the means of two groups and determine whether there is a significant difference between them. It is particularly useful when working with small sample sizes and when the population standard deviation is unknown. The t-test is based on the t-distribution and is widely employed in hypothesis testing and statistical inference.
There are different types of t-tests, but two of the most common ones are:
- Independent Samples t-test: Used to compare the means of two independent groups to assess whether there is a statistically significant difference between them. It assumes that the data in each group are independent and approximately normally distributed.
The null hypothesis typically states that there is no difference between the means of the two groups, while the alternative hypothesis suggests that a significant difference exists.
The test statistic is calculated as:
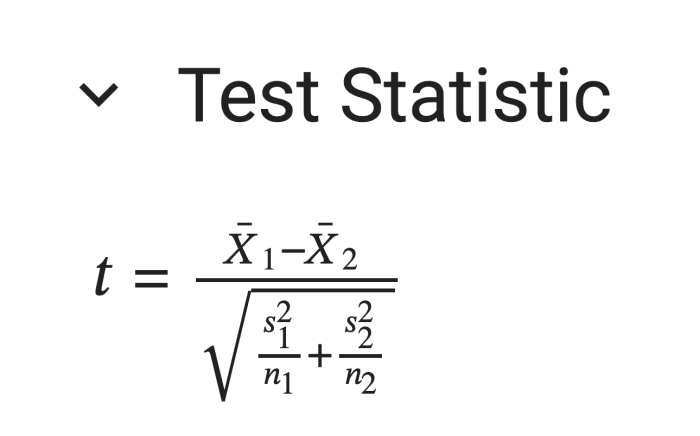
Here, X_1 and X_2 are the sample means, and s_1 and s_2 are the sample standard deviations, and n_1 and n_2 are the sample sizes.
- Paired Samples t-test:
Used when comparing the means of two related groups, such as repeated measurements on the same subjects or matched pairs. The test assesses whether the mean difference between paired observations is significantly different from zero.
The null hypothesis typically states that there is no difference in the means of the paired samples, while the alternative hypothesis suggests a significant difference.
The test statistic is calculated as:

Here, d is the mean of the differences, s_d is the standard deviation of the differences, and n is the number of pairs.
Key Uses of t-tests:
- Comparing Means: Assess whether the means of two groups (independent samples) or the mean difference within a single group (paired samples) are statistically different.
- Hypothesis Testing: Test hypotheses about population means based on sample data.
- Comparing Treatments in Experimental Design: Evaluate the effectiveness of different treatments or interventions in experimental studies.
- Quality Control: Assess whether changes in manufacturing processes or product formulations lead to significant differences in product characteristics.
- Before-and-After Studies: Evaluate whether there is a significant change in measurements before and after a particular treatment or intervention.
It's important to note that when conducting a t-test, assumptions such as normality of data and homogeneity of variances should be considered. Violations of these assumptions may affect the validity of the results, and alternative tests or adjustments may be needed.